Бильярдная физика | test4some

Бильярдная физика (продолжение)

Движение шара представляет собой комбинацию поступательного и вращательного движений.
Движение шара можно разложить на поступательное движение его центра масс под действием внешних сил и вращение относительно центра масс под действием моментов этих сил.
Вращение в трёхмерном пространстве — это вращение на определённый угол вокруг определённой оси.
При рассмотрении движения шара используют две системы координат Oxyz: неподвижная система координат и подвижная система координат. Вращательное движение шара вокруг точки - движение шара, при котором какая-то одна его точка остается неподвижной (центр масс), а все другие точки движутся по поверхности сфер, имеющих центр в этой точке. При таком вращательном движении шара любые его элементарные перемещения представляют собой элементарный поворот вокруг некоторой оси, проходящей через центр масс - мгновенная ось вращения.
Т.о. вращение шара вокруг центра масс в системе центра масс - вращение вокруг мгновенной оси, проходящей через этот центр с мгновенной угловой скоростью (ω).
Кинематика вращения вокруг неподвижной точки характеризуется вектором мгновенной угловой скорости.
Угловая скорость (ω) — это векторная величина, определяющая быстроту изменения угла поворота тела относительно оси вращения. Вектор угловой скорости направлен вдоль оси вращения в ту сторону, откуда вращение видно происходящим против хода часовой стрелки. Такой вектор определяет сразу и модуль угловой скорости, и ось вращения и направление вращения вокруг этой оси.
При ударе кием не направленным в центр шара, шар получает от кия не только импульс, который приводит шар в поступательное движение, но и момент импульса, который приводит шар во вращательное движение.
Импульс характеризует количество поступательного движения. Изменение импульса шара при ударе равно импульсу ударной силы (ударному импульсу).
[Силы, действующие на тела, можно разделить на силы, изменяющие скорость точек непрерывно и силы, изменяющие скорости точек тела в течение очень малого промежутка времени, такие силы возникают при ударе и называются ударными силами.
Ударные силы, будучи равными нулю в начале и конце удара, в процессе соударения изменяются в значительных пределах. В теории удара изменение импульса тела равно импульсу средней силы, действующей на тело. Импульс силы, мера действия силы за некоторый промежуток времени. Ударный импульс, импульс ударной силы, действующий на каждое из соударяющихся тел при ударе. Ударный импульс, равняется произведению среднего значения силы Fср на время tуд её действия: F^=Fср*tуд] Поступательная скорость шара за время контакта кия с шаром увеличиваются от нуля до той скорости с которой шар начинает двигаться сразу после удара (V) - шар получает от кия импульс, который приводит шар в поступательное движение.
F^=m*V
V - поступательная скорость шара - скорость центра масс шара (сразу после удара).
F^ - импульс ударной силы.
Момент импульса характеризует количество вращательного движения. Изменение момента импульса шара относительно центра (О) при ударе равно моменту ударного импульса.
Вращательная скорость шара за время контакта кия с шаром увеличиваются от нуля до той скорости с которой шар начинает вращаться вокруг центра масс сразу после удара (ω) - шар получает от кия момент импульса, который приводит шар во вращательное движение.
Вращение шара вокруг центра масс - вращение вокруг мгновенной оси, проходящей через этот центр с мгновенной угловой скоростью (ω).
Вращение вокруг оси проходящей через центр масс рассматривается в той системе отсчета, в которой она покоится (системе центра масс)
Для описания вращения достаточно рассмотреть проекции векторов моментов импульса и силы на ось вращения.
Момент импульса тела весьма сложно зависит от распределения масс в теле. Его направление в общем случае не совпадает с направлением угловой скорости вращения.
Для тела любой формы и с произвольным распределением массы существуют три взаимно перпендикулярные, проходящие через центр инерции тела оси (центр масс), которые могут служить свободными осями. Свободной осью тела называется ось вращения, положение которой в пространстве сохраняется без действия на нее каких-либо сил извне. Такие оси называют главными осями инерции тела. Совпадение направлений векторов момента импульса и угловой скорости будет тогда, когда угловая скорость направлена вдоль одной главных осей инерции тела.
Все оси симметрии твердого тела являются главными осями инерции. У тела с центральной симметрией ни одна из главных осей не фиксирована, ими могут служить любые три взаимно перпендикулярные оси, проходящие через центр симметрии. Для этих осей моменты инерции равны. Такое тело называется шаровым волчком. Это значит, что любая ось, проходящая через центр масс шара, будет главной осью инерции (осью свободного вращения), т.о. при любом направлении вектора мгновенной угловой скорости вектор момента импульса будет совпадать с ним по направлению.
В данном случае, L_=I*ω_
Поместим начало координат в центр шара ((.) O), тогда Ox, Oy и Oz - оси координат - главные оси инерции шара.
Сумма вращений относительно пересекающихся в одной точке осей представляет собой вращение вокруг мгновенной оси. Соответственно верно и обратное, математически в каждый момент вращение вокруг (единственной) мгновенной оси можно разложить на ряд вращений вокруг осей, пересекающихся в одной точке.
ω_=ω_x+ω_y+ω_z
|ω|=ωx2+ωy2+ωz2
ωx, ωy, ωz - cоставляющие вектора угловой скорости относительно центра по осям координат.
Направление мгновенной оси вращения определяется вектором, равным геометрической сумме векторов угловых скоростей составляющих движений.
Произведение Ix*ω_x дает составляющую вектора момента импульса по оси x.
Произведение Iy*ω_y дает составляющую вектора момента импульса по оси y.
Произведение Iz*ω_z дает составляющую вектора момента импульса по оси z.
L_=L_x+L_y+L_z=Ix*ω_x+Iy*ω_y+Iz*ω_z
Результирующий вектор момента импульса L_ будет совпадать по направлению с вектором ω_ если моменты инерции относительно главных осей Ix, Iy, Iz равны между собой, либо вектор ω_ направлен по одной из главных осей, тогда составляющие ω_ по остальным осям будут равны нулю.
Для шара: Ix=Iy=Iz=I
L_=I*(ω_x+ω_y+ω_z)=I*ω_
ω - угловая скорость шара относительно данной главной оси инерции (мгновенная угловая скорость) - угловая скорость относительно центра масс.
I - момент инерции однородного шара относительно любой главной оси инерции - любой оси, проходящей через центр масс.
I=25mR2
Причиной изменения момента импульса является действующий на систему результирующий момент внешних сил.
Моментом силы называют вращательное усилие создаваемое вектором силы относительно оси или точки.
Моментом силы F_ относительно точки O называется вектор M_o(F_) равный векторному произведению радиуса-вектора r_, проведенного из точки O в точку приложения силы, и вектора силы F_.
M_o(F_)=[r_xF_]
Вектор M_o(F_) приложен в точке O и направлен перпендикулярно плоскости, проходящей через центр O и силу F_ (то есть плоскости в которой лежат векторы r_ и F_), в ту сторону, откуда сила видна стремящейся повернуть тело вокруг центра O против хода часовой стрелки.
Модуль момента силы относительно точки равен произведению силы |F_| на плечо d.
|M_o(F_)|=|F_|*d
d - плечо силы относительно точки (кратчайшее расстояние от данной точки до линии действия силы, т. е. длина перпендикуляра, опущенного из этой точки на линию действия силы.)
Точка O - центр масс шара.
Момент силы относительно точки - это вектор, момент относительно оси - скаляр - проекция на эту ось векторного момента силы относительно любой точки на оси.
Момент силы относительно оси будет иметь знак плюс, когда с положительного конца оси тело под действием заданной силы представляется вращаю­щимся вокруг оси против хода часовой стрелки, и знак минус - когда по ходу часовой.
Изменение момента импульса шара относительно центра (О) при ударе равно моменту ударного импульса.
Вращательная скорость шара за время контакта кия с шаром увеличиваются от нуля до той скорости с которой шар начинает вращаться сразу после удара (ω). [Вращение вокруг мгновенной оси проходящей через центр масс в системе центра масс]
Т.о шар получает от кия момент импульса, который приводит шар во вращательное движение.
Для шара любая ось, проходящая через центр масс будет главной осью инерции, т.о. при любом направлении вектора угловой скорости вектор момента импульса будет совпадать с ним по направлению.
В данном случае вектор момента силы направлен по мгновенной оси вращения, проекция векторного момента силы на ось будет равна модулю момента силы относительно точки, взятому с соответствующим знаком.
I*ω_=M_o(F_)=[r_xF_]
I*ω=+|M_o(F_)|=+|F_|*d
В качестве силы F рассматривается ударный импульс F^
ω - угловая скорость шара относительно центра масс шара (сразу после удара).
I - момент инерции однородного шара относительно любой оси проходящей через центр масс.
F^*d - момент ударного импульса относительно центра.
d - плечо силы относительно центра масс - кратчайшее расстояние от данной точки (центра) до линии действия силы, т. е. длина перпендикуляра, опущенного из этой точки на линию действия силы
[центр масс однородного шара – центр симметрии шара - центр шара]
Поступательная и вращательная скорости шара за время контакта кия с шаром увеличиваются от нуля до тех скоростей с которыми начинает двигаться биток сразу после удара (V и ω).
{F^=m*V+|F^|*d=I*ω --- |ωRV|=52dR - отношение вращательной скорости относительно центра (линейная скорость вращения точки опоры) к поступательной.
Вращение вокруг неподвижной точки можно свести к трем независимым вращениям вокруг трех взаимно перпендикулярных осей - главных осей инерции.
Для шара направления главных осей инерции может быть выбрано произвольно - любая тройка взаимно перпендикулярных осей с началом в центре масс. Все три главных момента инерции совпадают: Оси системы координат Охyz, связанной с центром масс шара и совершающей поступательное движение вместе с ним, будут главными осями инерции.
Момент силы относительно центра складывается из моментов этой силы относительно трех взаимно перпендикулярных осей. (Любой вектор в трехмерном пространстве можно разложить единственным образом по любым трем некомпланарным векторам.)
(.) O - начало декартовой системы координат - центр шара.
|M_o|=Mx2+My2+Mz2
Момент силы относительно оси - проекция на эту ось момента силы относительно любой точки на оси – алгебраический момент проекции силы на плоскость, перпендикулярную к оси, относительно точки пересечения оси с этой плоскостью (O1).
Момент силы относительно оси будет иметь знак плюс, когда с положительного конца оси тело под действием заданной силы представляется вращаю­щимся вокруг оси против хода часовой стрелки, и знак минус - когда по ходу часовой.
[Если взять в качестве рассматриваемых плоскостей проекций координатные плоскости XY,XZ,YZ, то точкой пересечения осей X,Y,Z с плоскостями YZ,XZ,XY, соответственно, будет точка O - начало системы координат. (.)O1=(.)O]
{Mx(F_)=Mo1(F_yz)=+|F_yz|*dxMy(F_)=Mo1(F_xz)=+|F_xz|*dyMz(F_)=Mo1(F_xy)=+|F_xy|*dz
{+|F_yz|*dx=I*ωx+|F_xz|*dy=I*ωy+|F_xy|*dz=I*ωz
{ a { b (a,b) z x O
Горизонтальная плоскость - воображаемая плоскость, проходящая через биток параллельно поверхности стола
Вертикальная плоскость - воображаемая плоскость, проходящая через биток перпендикулярно поверхности стола
Разложение вектора момента силы относительно точки по осям X,Y,Z.
Геометрический способ вычисления момента
    Момент силы относительно оси: (x,y,z)
  1. провести плоскость H, перпендикулярную оси - в любом месте.
  2. спроецировать силу F_ на эту плоскость и найти F_H
  3. опустить из точки пересечения оси с плоскостью (O1) перпендикуляр на линию действия силы F_H и найти длину dH.
  4. вычислить произведение модуля проекции силы на плечо |F_H|*dH
  5. определить знак момента:
    Момент считается положительным, если проекция силы на плоскость, перпендикулярную к оси, стремится вращать тело вокруг положительного направления оси против движения часовой стрелки, и отрицательным, если она стремится вращать тело по движению часовой стрелки
O1
C
D
▲
E
↨
|a|
|b|
O
R
O
x
y
z
G
Рис.1
O1
C
D
▲
↨
|a|
|b|
O
R
O
x
y
z
R - радиус шара
|a| - расстояние от точки удара до координатной плоскости YZ.
|b| - расстояние от точки удара до координатной плоскости XY.
где центр шара (O) - начало системы координат.
Ось Y - по направлению движения шара, ось X перпендикулярно ей в горизонтальной плоскости, ось Z - вверх, перпендикулярно плоскости OXY.
a и b - координаты по осям OX и OZ соответственно
▲
- приложенная сила удара
Момент силы F_ относительно оси OX
H
1) H - плоскость, перпендикулярная оси OX. Для шара с центром в начале координат сечение шара плоскостью перпендикулярной оси OX на расстоянии |a| от оси Х.
2) В этом случае проекция F_H равна самой силе F_
F_H=F_
3) (.) O1 - точка пересечения оси OX с плоскостью H (центр малого сечения шара)
DO1 - радиус малого сечения шара
DO1=R2-a2
CO1=|b|
∠CDE=∠θ - угол наклона кия (рад)
∠CDO1=arcsin(|b|R2-a2)
∠O1DE=∠CDE-∠CDO1=θ-arcsin(|b|R2-a2)
Если бы линия дествия силы (линия кия) проходила выше центра масс:
O1 C D E b ▲
∠O1DE=∠CDO1-∠CDE=arcsin(|b|R2-a2)-θ
Если бы точка приложения силы находилась ниже центра масс:
O1 C D E b ▲
∠O1DE=∠CDE+∠CDO1=θ+arcsin(|b|R2-a2)
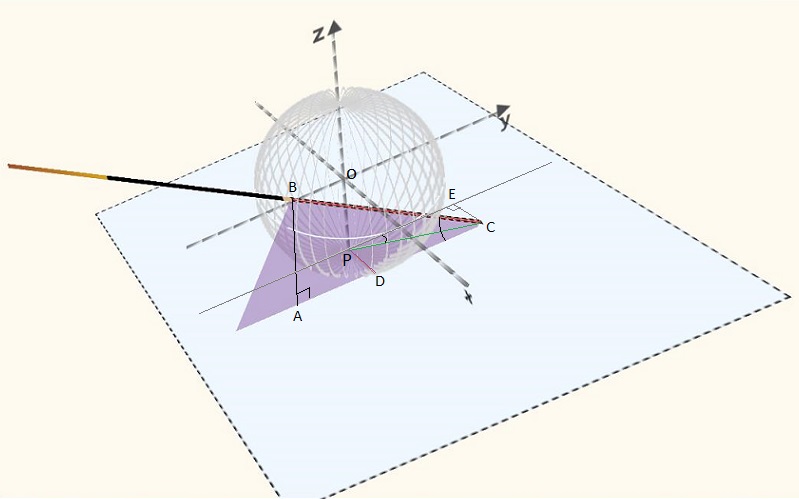
Рассмотрим случай когда точка приложения силы находится выше центра масс, линия дествия силы проходит ниже центра масс (Рис.1)
∠O1DE=∠CDE-∠CDO1=θ-arcsin(|b|R2-a2)
EO1=DO1*sin(∠O1DE) =(R2-a2)*sin(θ-arcsin(|b|R2-a2))
Details
=(R2-a2)*(sin(θ)*cos(arcsin(|b|R2-a2))-sin(arcsin(|b|R2-a2))*cos(θ))
=(R2-a2)*(sin(θ)*1-sin2(arcsin(|b|R2-a2))-(|b|R2-a2)*cos(θ))
=(R2-a2)*(sin(θ)*1-b2R2-a2-(|b|R2-a2)*cos(θ))
=sin(θ)*R2-a2-b2-|b|*cos(θ)
- точка приложения силы находится выше центра масс, линия дествия силы проходит ниже центра масс
Details Можно найти EO1 другим способом:
Рассмотрим ΔCDG.
sin(θ)=b+O1GDG cos(θ)=DCDG
DC=|y| |y|=R2-a2-b2
EO1=O1G*sin(90-θ)=O1G*cos(θ)
O1G=EO1cos(θ)
DG=b+O1Gsin(θ)=|y|cos(θ)
(b+EO1cos(θ))*cos(θ)=|y|*sin(θ)
b*cos(θ)+EO1=|y|*sin(θ)
EO1=sin(θ)*R2-a2-b2-|b|*cos(θ)
EO1=|b|*cos(θ)-sin(θ)*R2-a2-b2
- точка приложения силы находится выше центра масс, линия дествия силы проходит выше центра масс
EO1=sin(θ)*R2-a2-b2+|b|*cos(θ)
- точка приложения силы находится ниже центра масс
dx=EO1 - плечо силы относительно оси OX
4) |F_|*dx
5) Знак момента:
Mx(F_)=|F|_*(sin(θ)*R2-a2-b2-|b|*cos(θ))
Знак момента: +
- точка приложения силы находится выше центра масс, линия дествия силы проходит ниже центра масс (b>0)
Mx(F_)=-|F|_*(|b|*cos(θ)-sin(θ)*R2-a2-b2)
Знак момента: -
- точка приложения силы находится выше центра масс, линия дествия силы проходит выше центра масс (b>0)
Mx(F_)=|F|_*(sin(θ)*R2-a2-b2+|b|*cos(θ))
Знак момента: +
- точка приложения силы находится ниже центра масс (b<0)
Объединяя все случаи:
Mx(F_)=|F|_*(sin(θ)*R2-a2-b2-b*cos(θ))
где: a и b - координаты по осям OX и OZ соответственно
Частный случай:
Если ∠θ=0 - горизонтальный кий, то: dx=EO1=b
Момент силы F_ относительно оси OY
Для определения момента относительно оси OY в качестве плоскости H удобно принять координатную плоскость OXZ. Тогда:
|F_H|=|F_|*sin(θ)
dy=|a| - плечо силы относительно оси OY
Знак момента: + если точка приложения силы находится правее центра масс
My(F_)=|F|_*sin(θ)*|a|
Знак момента: - если точка приложения силы находится левее центра масс
My(F_)=-|F|_*sin(θ)*|a|
Момент силы F_ относительно оси OZ
Для определения момента относительно оси OZ в качестве плоскости H удобно принять координатную плоскость OXY. Тогда:
|F_H|=|F_|*cos(θ)
dz=|a| - плечо силы относительно оси OY
Знак момента: + если точка приложения силы находится правее центра масс
My(F_)=|F|_*cos(θ)*|a|
Знак момента: - если точка приложения силы находится левее центра масс
My(F_)=-|F|_*cos(θ)*|a|

Аналитический способ вычисления момента
(x,y,z) a b R F_ θ (
R-радиус шара
R=x2+y2+z2
x=a
y=-R2-x2-z2=-R2-a2-b2
z=b
F_-вектор силы
θ-наклон кия
Моменты силы F_ относительно трех координатных осей x,y,z:
{Mx(F_)=y*Fz-z*FyMy(F_)=z*Fx-x*FzMz(F_)=x*Fy-y*Fx
где -
x,y,z - координаты точки приложения силы F_
Fx, Fy, Fz - проекции силы F_ на координатные оси
При аналитическом способе вычисления осевых моментов необходимо определить проекции силы на координатные оси и проекции радиуса-вектора точки приложения силы.
F_=(0;|F|_*cos(θ);-|F|_*sin(θ))
R_=(a;-R2-a2-b2;b)
------
{Mx(F_)=(-R2-a2-b2)*(-|F|_*sin(θ))-b*(|F|_*cos(θ))=|F|_*(sin(θ)*R2-a2-b2-b*cos(θ))=+|F_|*dxMy(F_)=b*0-a*(-|F|_*sin(θ))=|F|_*sin(θ)*a=+|F_|*sin(θ)*dyMz(F_)=a*(|F|_*cos(θ))-(-R2-a2-b2)*0=|F|_*cos(θ)*a=+|F_|*cos(θ)*dz
Details
В данном случае мы рассматриваем точки удара на ближайшей к нам стороне от центрального сечения шара, т.е y=-R2-a2-b2<0

[точка O - центр шара - начало декартовой системы координат]
Если рассмотреть точки удара на другой (дальней от нас) стороне от центрального сечения шара, тогда y=+R2-a2-b2>0
Теоретически, такой удар можно нанести наклонным кием. Но в эти точки в бильярде наносить удар не имеет смысла. Велика вероятность повторного столкновения кия с битком. [точка O - центр шара - начало декартовой системы координат]
Есть и самый простой способ выразить плечо силы относительно оси (X,Y,Z) через координаты точки удара (x,y,z) = (a,y,b) и наклон кия (∠θ).
Для этого надо рассмотреть удар горизонтальным кием в пределах зоны кикса (т.е круга радиуса 0,57*R), а пототом просто повернуть шар вокруг оси X по часовой стрелке на желаемый угол наклона кия.
До поворота (горизонтальный кий):
Вид сбоку:
Вид сверху:
R=x2+y2+z2=a2+y2+b12 Координаты (.) A (a, -R2-a2-b12 ,b1) При горизонтальном ударе плечо силы относительно каждой из осей:
  • X: dx=|b1|
  • Y: dy=|a|
  • Z: dz=|a|
После поворота (наклонный кий):
Вид сбоку: ∠θ - угол наклона кия
Вид сверху:
При повороте вокруг оси X - координата x не изменится (a); координата y в данном случае роли не играет; остается найти только новую координату z (b).
Матрица поворота (вокруг оси OX): (1000cos(-θ)-sin(-θ)0sin(-θ)cos(-θ))
Угол поворота: -θ (поворот по часовой стрелке)
Тогда:
[x`y`z`]=[1000cos(-θ)-sin(-θ)0sin(-θ)cos(-θ)]x[xyz] = [1000cos(-θ)-sin(-θ)0sin(-θ)cos(-θ)]x[a-R2-a2-b12b1]
z`=b= 0*a+sin(θ)*R2-a2-b12+cos(θ)*b1
(sin(θ)*R2-a2-b12)2 =(b-cos(θ)*b1)2
sin2(θ)*(R2-a2)-sin2(θ)*b12 =b2-2*b*cos(θ)*b1+cos2(θ)*b12
sin2(θ)*(R2-a2) =b2*(sin2(θ)+cos2(θ))-2*b*cos(θ)*b1 +b12*(sin2(θ)+cos2(θ))
sin2(θ)*(R2-a2-b2)=(cos(θ)*b-b1)2
Details
В данном случае мы рассматриваем точки удара на ближайшей к нам стороне от центрального сечения шара, т.е y=-R2-a2-b2<0

[точка O - центр шара - начало декартовой системы координат]
→ угол наклона кия (∠θ) имеет верхний предел θ<π2-arcsin(b1R2-a2) → ctg(θ)>b1R2-a2-b12 → (cos(θ)*b-b1)>0
b1=-sin(θ)*R2-a2-b2+b*cos(θ) dx=|b1|
Если b1>0, т.е. линия действия силы проходит выше центра масс:
dx=b1 dx=-sin(θ)*R2-a2-b2+b*cos(θ)
Если b1<0, т.е. линия действия силы проходит ниже центра масс:
dx=-b1 dx=sin(θ)*R2-a2-b2-b*cos(θ)
Таким образом, модуль момента силы относительно точки O (центра шара):
|MO_(F_)| =Mx(F_)2+My(F_)2+Mz(F_)2 =|F|_*d
,
где d - плечо силы F_ относительно точки O (центра масс шара)
F_ - ударный импульс (импульс ударной силы)
В бильярде плечо силы F_ относительно центра шара называют - tip offset - расстояние между центром битка и линией проходящей через точку удара параллельно направлению движения кия.
Данная величина ограничена зоной кикса (≈0,57R)
|MO_(F_)| =(|F|_*(sin(θ)*R2-a2-b2-b*cos(θ)))2+(|F|_*sin(θ)*a)2+(|F|_*cos(θ)*a)2 =|F|_*a2+(sin(θ)*R2-a2-b2-b*cos(θ))2
d(tip offset) = a2+(sin(θ)*R2-a2-b2-b*cos(θ))2
или
d(tip offset) = a2+((R2-a2)*sin(θ-arcsin(bR2-a2)))2
Тогда, принимая во внимание, что dlim≈0.57R
Для заданной точки удара (a,-R2-a2-b2,b) угол наклона кия (∠θ) изменяется в пределах:
(asin(bR2-a2)-asin((0.57*R)2-a2R2-a2)) <θ< (asin(bR2-a2)+asin((0.57*R)2-a2R2-a2))
где a и b - координаты точки удара, если поместить начало координат в центр шара.
Отсюда видно, что чем ниже точка удара относительно центра (b<0), тем меньше ∠θ для того, чтобы не получился кикс.
Или наоборот, чем больше наклон кия (∠θ), тем выше находятся точки на шаре в которые можно ударить без кикса (если смотреть с фронтальной проекции)
Наклон кия - 0°
Наклон кия - 15°
Наклон кия - 30°
Наклон кия - 45°
Наклон кия - 60°
Наклон кия - 75°

Для того, чтобы получить зону кикса необходимо представить сечение шара радиуса 0.57R во фронтальной плоскости проекций и затем мысленно повернуть шар вокруг оси OX на угол наклона кия.
Фронтальная плоскость проекций - плоскость, которая расположена вертикально и перпендикулярно взору наблюдателя Как говорят в бильярде - "поднимая" кий (подъем турняка кия, т.е наклон кия) также "поднимаешь" зону кикса.

Зона кикса
В том случае, если наклейка кия проскальзывает по поверхности битка из-за того, что удар нанесен слишком близко к краю, или из-за того, что на наклейке мало мела, то такой удар не будет верным. Такой удар называется кикс.
Так как при ударе нет скольжения кия по шару, частицы шара, получившие удар кием, сцепляются с кием и, пока продолжается соприкосновение, не могут иметь скоростей, отличных от скоростей ударяющих точек кия.
Такое "сцепление" при котром поверхности не дают друг другу скользить называется силой статического трения или силой трения покоя.
Силу трения покоя обычно называют силой сцепления, чтобы отличать от силы трения покоя, возникающей при контакте тел, не способных катиться. Силу трения покоя также называют статическим трением. Статическое трение — это сила, удерживающая объект в покое и препятствующая его движению, действующая до тех пор, пока приложенная сила не превысит силу статического трения. Кинетическое трение, также известное как трение скольжения или движущееся трение, действует на объект, когда он находится в движении.
Статическая сила трения колеблется от нуля до своего максимального предела, который является предельным трением. Предельное трение — это сила трения, приложенная в тот момент, когда тело собирается двигаться. Его формула выглядит следующим образом: Fтрп=μп*Fн,
где: Fтрп - предельное трение; μп - коэффициент статического трения; Fн - сила нормальной реакции.
Коэффициент трения равен тангенсу угла трения. Тангенс угла трения иногда коротко называют тангенсом трения.
Угол трения (∠α) - угол между силой (полная реакция поверхности - ударный мспульс) и нормалью к опорной поверхности.
tg(α)=FтрFн
Тело приходит в движение, когда внешняя сила равна предельной силе трения. И если внешняя сила превышает предельное трение, тело начинает двигаться.
Таким образом, если линия удара находится на таком расстоянии от центра шара, что линия действия силы (линия удара) образует угол с нормалью к поверхности шара превосходящий угол трения, то будет иметь скольжение конца кия по шару во время удара. Такой удар не будет верным.
Fтр^
Fн^
Fуд^
α
d
Предельный угол трения: tg(α)=FтрпFн≈0.7
Угол трения: tg(α)=sin(α)cos(α)=d/R1-(d/R)2<0.7
d/R<0.57
Шар получит в направлении удара кия количество движения, которое будет измеряться произведением массы шара на скорость его центра.
Сцепление между кием и шаром во время удара, приводит к тому, что количество движения, полученное шаром, всегда имеет направление скорости кия, а эта скорость не меняет заметно своего направления во время удара.
▲z
▲
▲
➤
▲
▲y
▲x
Min: 0 Max: 70
xyz xyz xyz
-17504 000 -9000
Вращать:
xyz
▲- Ударный импульс
▲- радиус-вектор
▲- Плечо силы относительно центра шара
▲- Момент силы относительно центра шара
➤- Ось вращения шара
- Кий
Вектор M_o(F_)=(Mx,My,Mz) лежит вдоль оси вращения.
(a,y,b) - координаты точки приложения силы F_
(.) O - центр шара; ∠ θ - угол наклона кия
Поместим в (.) O начало системы координат. [Координатные оси удобно взять так, что направление движения центра шара совпадает с положительным направлением оси Y, ось X - проведенная горизонтально перпендикулярно оси Y, ось Z - вертикально вверх. Координаты x и y лежат в поверхности, z перпендикулярно поверхности.] {Mx=|F|_*(sin(θ)*R2-a2-b2-b*cos(θ))My=|F|_*sin(θ)*aMz=|F|_*cos(θ)*a
Тогда:
∠ α - угол наклона мгновенной оси вращения к плоскости OXY (в момент времени t). ∠α=arctg(|ω`z|ω`x2+ω`y2)
∠ α - угол наклона мгновенной оси вращения к плоскости OXY (сразу послу удара кием).
∠α=arctg(|ωz|ωx2+ωy2) =arctg(|Mz|Mx2+My2) = arctg(cos(θ)*|a|(sin(θ)*R2-a2-b2-b*cos(θ))2+(sin(θ)*a)2)
∠ β - угол наклона мгновенной оси вращения к плоскости OXZ. ∠β=arctg(|ω`y|ω`x2+ω`z2)
∠ β - угол наклона мгновенной оси вращения к плоскости OXZ (сразу послу удара кием).
∠β=arctg(|ωy|ωx2+ωz2) =arctg(|My|Mx2+Mz2) =arctg(sin(θ)*|a|(sin(θ)*R2-a2-b2-b*cos(θ))2+(cos(θ)*a)2)
ω`x, ω`y, ω`z - угловые скорости относительно осей X,Y,Z в момент времени t.
ωx, ωy, ωz - угловые скорости относительно осей X,Y,Z сразу после удара кием.
Если My=|F|_*sin(θ)*a=0
То есть либо ∠ θ=0 (кий горизониальный); либо a=0 - то есть удар в вертикальной плоскости происходящей через центр шара, то ∠ β=0
При ударе горизонтальным кием в какой бы точке шара не был нанесен удар кием, ось вращения всегда лежит в плоскости перпендикулярной направлению поступательного движения, т.е в плоскости, образуемой осями X и Z. Ось вращения перпендикулярна направлению поступательного движения. [ωx,ωy=0,ωz]
При ударе наклонным кием, если вертикальная плоскость удара не проходит через центр шара, т.е. при ударе наклонным кием с боковой составляющей винта, ось вращения не перпендикулярна направлению поступательного движения. [ωx,ωy≠0,ωz]
▲
▲
▲
➤
X
Y
Z
O
ωx=MxI
ωy=MyI=0
ωz=MzI
α (
▲
▲
▲
➤
X
Y
Z
O
ωx=MxI
ωy=MyI
ωz=MzI
α(
β(
Таким образом, координаты a,b и угол наклона кия ∠ θ однозначно определяют соотношение скоростей поступательного (V) и вращательного (ω) движений битка сразу после удара. Относительно осей вращения X,Y,Z
{+|F_yz|*dx=I*ωx+|F_xz|*dy=I*ωy+|F_xy|*dz=I*ωz
{|F_yz|=|F_||F_xz|=|F_|*sin(θ)|F_xy|=|F_|*cos(θ)
|F_|=F^ - ударный импульс
F^=m*V
{|ωx*RV|=52dxR|ωy*RV|=52dyR*sin(θ)|ωz*RV|=52dzR*cos(θ)
{dx=|sin(θ)*R2-a2-b2-b*cos(θ)|dy=|a|dz=|a|
Принмая во внимание, что в случае удара наклонным кием поступательная скорость (V) направлена под углом (∠θ) к движению шара.
Vп=V*cos(θ)
[Vп - горизонтальная составляющая в поступательном движении шара]
    Рассмотрим некоторые правила (секреты) бильярда:
  • Удары наклейкой кия в точки на битке на линии исходящей из точки касания битка с сукном (точка опоры) приводят к качению с одним и тем же наклоном оси вращения, разница будет только в длине начальной фазы скольжения битка по сукну.
Рассмотрим удар в (.) C горизонтальным кием.
(.) C лежит на прямой исходящей из точки опоры (.) D под углом ξ к оси OZ (ось OY направлена от нас по линии кия) внутри отрезка AB, ограниченного зоной кикса.
(.) O - центр шара. R - радиус шара.
Пусть, DC=s
Тогда (.) С имеет координаты ( -s*sin(ξ),y,s*cos(ξ)-R )
При вращении луча против часовой стрелки считается, что его угол поворота положительный, т.е. луч вращается в положительном направлении.
При вращении луча по часовой стрелке считается, что его угол поворота отрицательный, т.е. луч вращается в отрицательном направлении.
[Т.е если (.) С правее (.) O (центр), то: ∠ξ<0; если (.) С левее (.) O (центр),то: ∠ξ>0]
dx=|s*cos(ξ)-R| [плечо силы относительно оси OX]
dz=|s*sin(ξ)| [плечо силы относительно оси OZ]
Тогда угол наклона оси вращения к плоскости OXY (∠ α) в момент когда шар достигнет финального состояния - качения: ∠α=arctg(|ωzf||ωxf|)=arctg(|ωzf*R||ωxf*R|)
где ωzf, ωxf - угловые скорости относительно осей OZ,OX к моменту финального качения шара.
Как известно, момент финального качения шара наступает когда линейная скорость вращения опорной точки (ω*R) равна и прямо противоположна поступательной скорости центра шара (Vп).
Как известно, финальная скорость шара (скорость к моменту финального качения) образуется на 57 от вектора начальной поступательной скорости (v_) и на 27 от вектора противоположного вектору начальной линейной скорости вращения опорной точки ([ω_xR_])
V_f=57V_0+27[ω_0xr_]
[Вектор r_ - вектор направленный из опорной точки в центр шара (r=-R)]
Подробнее (Бильярдная физика (часть №1))
Для правой системы координат, положительное вращение против часовой стрелки:
Vf=|ωxf*R|=57Vп-27ωx*R
где Vп, ωx - поступательная и угловая вращательная скорости (относительно оси OX) шара сразу после удара кием.
Моментом верчения, можно пренебречь по сравнению с моментом трения скольжения. ωzf*R=ωz*R
Тогда, принимая во внимание: {|ωx*RV|=52dxR|ωy*RV|=52dyR*sin(θ)|ωz*RV|=52dzR*cos(θ)Vп=V*cos(θ), ∠θ=0[горизонтальный кий] имеем:
|ωzf*Rωxf*R| =|ωz*R57Vп-27ωx*R| =|(ωz*R)/ωx*R(57Vп-27ωx*R)/ωx*R| =|ωz/ωx57(1ωx*R/V)-27| =|dz/dx27(R/dx)-27| =|dz27R-27dx| =72(|s*sin(ξ)|R-R+s*cos(ξ)) =72|tg(ξ)|
То есть угол наклона оси вращения к оси OX в финальном состоянии качения зависит только от ∠ ξ.
Из этого отношения видно, что чем больше ∠ ξ тем больше угол наклона оси вращения к оси OX в финальном состоянии качения, соответственно тем меньше угол наклона к оси OZ. Чем ближе ось вращения к оси OZ тем больше на шаре бокового вращения в данный момент.
Из этого следует еще одно правило бильярда - для того, чтобы донести максимальный боковой винт до далекого ПШ бить нужно не с максимальным боковиком, а с максимальным нижне-боковым винтом.
Эта линия может быть полезна при планировании удара с боковым винтом. Удар в точки на битке, лежащие на наклонной линии проходящей через точку касания битка с сукном даст один и тот же наклон оси вращения/качения. Поэтому варьируя силу удара можно достичь одинакового результата удара, нанося удар в разные точки на этой линии.
Но при этом удар в верхние точки будет с большим плечом силы относительно оси Z (dz), чем удар в нижние точки. Увеличение плеча (dz) даст большее угловое отклонение битка (squirt), что нежелательно. Поэтому если позволяет расстояние до ПШ, то лучше наносить удар в нижние точки (по линии), добавив силу удара. То есть результат удара в верхнюю точку по линии (с большим смещением от центра битка) и более сильного удара в нижнюю точку на линии (с малым смещением от центра битка) будет одинаков. Разница будет только в длине фазы скольжения битка по сукну, и в величине эффекта сноса. Но, здесь надо отметить, что для того, чтобы это правило работало биток к моменту соударения с ПШ должен достигнуть состояния качения. Поэтому возможность удара в нижние точки (по линии) ограничена расстоянием до ПШ. При более низком и сильном ударе фаза скольжения битка удлиняется и шар может не успеть перейти в качение к моменту соударения с ПШ.
x y z
Изменение скорости и сам вид движения связаны с действием силы. Если на тело действует сила, то тело изменяет свою скорость, направление движения или и то, и другое. Если сила направлена параллельно движению тела, то такое движение будет прямолинейным. Криволинейным будет такое движение, когда скорость тела и сила, приложенная к этому телу, направлены друг относительно друга под некоторым углом. В этом случае скорость будет изменять свое направление. В нашем случае сила, изменяющая скорость/направление движения шара – это сила трения. Сила трения приложена к точке соприкосновения тела с поверхностью. Точка опоры шара - точка, которой шар касается сукна и к которой приложена сила трения.
Два рода трения: трение скольжения - проявляется когда шар скользит по сукну бильярда (переменное движение) и трение качения в финальном состоянии движения шара (финальное движение). Будем считать контакт точечным - трением верчения можно пренебречь. Трение скольжения действует противоположно скорости скольжения по сукну опорной точки шара. Скорость скольжения опорной точки шара обладает двумя скоростями поступательного и вращательного движения. V_ск=V_п+V_вр
Вектор линейной скорости вращения (V_вр) точки равен векторному произведению вектора угловой скорости (ω_) и радиус-вектора точки (R_).
V_вр=[ω_xR_]
Вектор линейной скорости вращения (V_вр) точки складывется из векторов [ω_xxR_], [ω_yxR_], [ω_zxR_]. , где R_ - радиус-вектор, проведённый из центра шара в точку.
В данном случае рассматриваем точку касания с плоскостью - точку опоры (т.е точку где приложена сила трения).
[ω_zxR_]=0, так как радиус вектор коллинеарен ω_z.
Вектор [ω_xxR_] направлен по оси OY.
Вектор [ω_yxR_] направлен по оси OX.
V_вр=[ω_xxR_]+[ω_yxR_]
Vвр=(ωx*R)2+(ωy*R)2
Таким образом, если ωy=0, то вектора линейной вращательной и поступательной скоростей точки опоры будут коллинеарны: т.е. при ударе горизонтальным кием (∠ θ=0), или при ударе в вертикальной плоскости, проходящей через центр шара (dy=0). В этом случае движение шара будет прямолинейным.
Если ωy≠0, то вектора линейной вращательной и поступательной скоростей точки опоры не будут коллинеарны: т.е при ударе наклонным кием с боковой составляющей винта. Вектор скорости скольжения (сумма векторов поступательного и вращательного движений), а следовательно и вектор силы трения, а следовательно и вектор ускорения будут направлены под углом к скорости поступательного движения. В этом случае движения шара будет криволинейным (параболическим).
Если при наклонной линии удара вертикальная плоскость удара не проходит через центр, то шар вначале опишет часть параболы переменным движением, после чего он перейдет в финальное состояние качения, следуя по касательной к этой кривой. Направление этой касательной нисколько не зависит от величины трения между бильярдным сукном и шаром.
Правило Кориолиса Чтобы получить направление шара в финальном состоянии (т.е когда он начинает катиться по прямой), необходимо представить, что линия удара (BC) продолжена до встречи с сукном в точке C. Проведем на сукне прямую, идущую от опорной точки шара (P) до C - полученное направление будет параллельно линии движения шара в его финальном состоянии (PC).
→
Финальный угол отклонения битка можно найти посмотрев наклон траектории в момент времени окончания скольжения.
Финальный угол отклонения шара равен:
∠δ=arctg(57Vx+27ωy*R57Vy-27ωx*R),
где:
Vx, Vy - проекции начальной поступательной скорости Vп [горизонтальная составляющая в поступательном движении шара] (сразу после удара кием) на оси OX, OY.
ωx, ωy - начальные угловые скорости вращения (сразу после удара кием) относительно осей OX, OY.
Оcь OY направлена по движению шара.
Учтем, что Vx=0 (без учета squirt - угловое отклонение 2-3 градуса).
Vy=Vп
Подробнее (Бильярдная физика (часть №1))
Тогда, принимая во внимание: {|ωx*RV|=52dxR|ωy*RV|=52dyR*sin(θ)|ωz*RV|=52dzR*cos(θ), Vп=V*cos(θ) имеем:
  • Если линия действия силы (BC) проходит ниже центра масс (O) → тогда вращение относительно оси OX - обратное (нижнее) → ωx>0 [для правой системы координат] → ωx*RV=52dxR
∠δ=arctg(2*ωy*R5*Vy-2*ωx*R) =arctg(2*ωy*R/ωx*R(5*Vy-2*ωx*R)/ωx*R) =arctg(2*(ωy/ωx)5*(1ωx*R/V)*cos(θ)-2) =+.arctg(2*(dy/dx)*sin(θ)2*(R/dx)*cos(θ)-2) =+.arctg(dy*sin(θ)R*cos(θ)-dx)
  • Если линия действия силы (BC) проходит выше центра масс (O) → тогда вращение относительно оси OX - прямое (верхнее) → ωx<0 [для правой системы координат] → ωx*RV=-52dxR
∠δ=+.arctg(dy*sin(θ)R*cos(θ)+dx)
Знак угла ∠δ - будет зависеть от знака ωy (правое/левое боковое вращение) и будет определять правое/левое финальное отклонение битка - в сторону примененного бокового винта.
В данном случае для дальнейшего анализа знак ∠δ роли играть не будет.
Рассмотрим △ABC.
∠EPC=arctg(ECPE)
(.) B имеет координаты ( a ; -R2-a2-b2 ; b )
AB=R+b
∠ BCA= ∠θ - угол наклона кия
AC=ABtg(θ)=R+btg(θ)
PE=DC
AC=AD+DC; DC=AC-AD;
AD=R2-a2-b2
DC=R+btg(θ)-R2-a2-b2
EC=|a|=dy
ECPE=ECDC=|a|R+btg(θ)-R2-a2-b2 =(|a|*tg(θ))*cos(θ)(R+b-tg(θ)*R2-a2-b2)*cos(θ) =|a|*sin(θ)R*cos(θ)-(sin(θ)*R2-a2-b2-b*cos(θ))
  • Если линия действия силы (BC) проходит ниже центра масс (O) → тогда вращение относительно оси OX - обратное (нижнее) → плечо силы относительно оси OX:
    dx=(sin(θ)*R2-a2-b2-b*cos(θ))
    →
    ∠EPC=∠δ=arctg(dy*sin(θ)R*cos(θ)-dx)
  • Если линия действия силы (BC) проходит выше центра масс (O) → тогда вращение относительно оси OX - прямое (верхнее) → плечо силы относительно оси OX:
    dx=(-sin(θ)*R2-a2-b2+b*cos(θ))
    →
    ∠EPC=∠δ=arctg(dy*sin(θ)R*cos(θ)+dx)
Длина криволинейной части траектории (но не направление) зависит от величины силы трения шара о бильярдное сукно, а также от силы удара.
Таким образом, финальное направление движения шара будет параллельно линии, идущей от его точки опоры к той точке, в которой линия удара пересекает плоскость бильярдного сукна.
На основании этого - если линия удара пересечет плоскость бильярда по эту сторону опорной точки, то шар должен будет пойти назад, двигаясь в направлении, противоположном направлению начальной скорости.
Рассмотрим случай, когда шар при ударе кием приобретает обратное (нижнее) вращение. Такое возможно при ударе кием, когда линия удара проходит ниже центра (центра масс).
Рассмотрим удар, когда вертикальная плоскость удара проходит через центр. То есть при ударе отсутствует боковая составляющая винта (dy=dz=|a|=0, ωy=ωz=0 ).
В данном случае движение будет прямолинейным.
Горизонтальный кий
Наклонный кий
В бильярде удар наклонным кием с нижним винтом (ниже цетра масс) в отсутствии боковой составляющей называется наклонной оттяжкой.
При ударе кием, когда линия проходит ниже центра шар начинает скользить, вращаясь в обратном направлении.
Сила трения скольжения тормозит как поступательное движение, так и вращение шара.
    В дальнейшем возможны 3 случая:
  1. Может случиться так, что поступательное движение шара будет остановлено в тот момент, когда он еще сохранит обратное вращение.
    Далее сила трения начнет ускорять шар в обратном направлении. Ставшее уже прямым (по направлению движения шара) вращение уменьшается, увеличивая при этом поступательную скорость Ускорение это прекратиться, когда исчезнет тенденция к проскальзыванию (т.е. поступательная и вращательная скорости точки опоры будут равны по модулю и противоположны по направлению). После чего шар перейдет в финальное состояние качения.
    То есть, в данном случае изменится направление поступательного движения
    ---
  2. Может случиться так, что поступательное движение шара и обратное вращение шара будут остановлены одновременно. Тогда шар остановится и фаза качения не наступит.
  3. Может случиться так, что раньше будет остановлено обратное вращение и тогда шар сохранит поступательное движение вперед, изменив направление вращения на прямое (верхнее). То есть, в данном случае изменится направление вращательного движения
Первые два случая невозможны при ударе горизонтальным кием, но возможны при ударе наклонным кием, когда линия удара пересечет плоскость бильярда по эту сторону опорной точки.
Рассмотрим поступательную и вращательную скорости опорной точки сразу после удара кием. [Координатные оси удобно взять так, что направление движения центра шара совпадает с положительным направлением оси Y, ось X - проведенная горизонтально перпендикулярно оси Y, ось Z - вертикально вверх. Координаты x и y лежат в поверхности, z перпендикулярно поверхности.]
Vп - поступательная скорость [горизонтальная составляющая в поступательном движении шара]
Vпx=0 [без учета небольшого углового отклонения squirt - 2-3°]
Vпy=Vп
Vвр=(ωx*R)2+(ωy*R)2 - вращательная скорость (линейная скорость вращения) [точки опоры]
Vврx=ωy*R
Vврy=ωx*R
|ωx*RV|=ωx*RV=52dxR, Vп=V*cos(θ)
tск=27Vотнµ*g - время скольжения
Vотн__=Vп__+Vвр__ - относительная скорость скольжения (вектор)
Vотн=Vотнx2+Vотнy2
Vотнx=Vпx-ωy*R - проекция Vотн на ось X
Vотнy=Vпy+ωx*R - проекция Vотн на ось Y
aпx=-µ*g*(VотнxVотн) - ускорение поступательного движения - проекция на ось Y
aврx=-52µ*g*(VотнxVотн) - линейное ускорение вращательного движения - проекция на ось Y
aпy=-µ*g*(VотнyVотн) - ускорение поступательного движения - проекция на ось Y
aврy=-52µ*g*(VотнyVотн) - линейное ускорение вращательного движения - проекция на ось Y
Подробнее (Бильярдная физика (часть №1))
Нужно рассмотреть какая из скоростей: поступательного или вращательного движения [в проекции на ось Y] поменяет свой знак за время скольжения. Vпy^Vврy за время tск.
Вращательная скорость (линейная) сразу после удара кием:
Vврy=ωx*R>0 [оттяжка (нижнее вращение), правая система координат]
Вращательная скорость (линейная) сразу после окончания фазы скольжения:
ωx*R+aврy*tск =ωx*R-(52µ*g*(VотнyVотн))*(27Vотнµ*g) =ωx*R-57Vотнy =ωx*R-57(V*cos(θ)+ωx*R) =27ωx*R-57V*cos(θ)
Таким образом, если 27ωx*R-57V*cos(θ) будет больше нуля, то к окончанию фазы скольжения нижнее вращение останется на шаре, и поступательная скорость [по оси Y] поменяет знак - изменит направление на противоположное.
Если 27ωx*R-57V*cos(θ) будет меньше нуля, то - наоборот.
Таким образом, получаем первое неравенство:
(ωx*RV*cos(θ))^52
-----
((dx/R)cos(θ))^1
Второе неравенство - это ограничение зоны кикса:
dy2+dx2<0.57*R
Таким образом данная система двух неравенств {((dx/R)cos(θ))^1dy2+dx2<0.57*R охватывает все три случая.
{dx=sin(θ)*R2-a2-b2-b*cos(θ)dy=|a|dz=|a|
При заданном наклоне кия (∠θ) из множества точек с координатами (a, -R2-a2-b2, b ) [( 0, -R2-b2, b ) - если вертикальная плоскость удара проходит через центр шара], ограниченных вторым неравенством (зоной кикса) -
знак первого неравенства разграничит три описывемых случая.
  1. знак> - первый случай, первым будет остановлено поступательное движение [проекция по оси Y] - шар пойдет назад
    Если вертикальная плоскость удара проходит через центр шара.
    {((dx/R)cos(θ))^1dx<0.57*R
    {dx=sin(θ)*R2-b2-b*cos(θ)dy=0dz=0
  2. знак= - второй случай, поступательное и вращательное движения будут остановлены одновременно - шар остановится
  3. знак< - третий случай, первым будет остановлено обратное вращение - шар пойдет вперед
Из первого неравенства видно, что при ударе горизонтальным кием (∠θ=0) неравенство принимает вид: (dx/R)<1
Наклон кия - 0°
Наклон кия - 45°
Наклон кия - 60°
Наклон кия - 70°
Наклон кия - 75°
Наклон кия - 80°
Полученное соотношение легко увидеть, воспользовавшись правилом Кориолиса - если линия удара пересечет плоскость бильярда по эту сторону опорной точки, то шар должен будет пойти назад, двигаясь в направлении, противоположном направлению начальной скорости.
O P θ α A dx R
Рассмотрим центральное сечение шара в профильной плоскости.
Проведем прямую из опорной точки P под углом ∠α на расстоянии dx от точки O (центра шара).
AP - линия действия силы.
dx - плечо силы
∠θ - угол наклона кия; OP=R
sin(α)=dxR
θ=90-α
sin(α)=sin(90-θ)=cos(θ)=dxR
Отсюда видно, что →
если линия удара пересечет плоскость бильярда по эту сторону опорной точки, то при заданном dx (<0.57R) ∠θ будет увеличиваться, cos(θ) уменьшаться → cos(θ)<dxR
если линия удара пересечет плоскость бильярда по ту сторону опорной точки, то - наоборот.
Выражения ускорения для поступательного и вращательного движений {aп=-µ*g- ускорение поступательного движенияaвр=-52µ*g- линейное ускорение вращательного движения верны для шара, который скользит, не отрываясь от поверхности стола (т.е без подскока)
Для ударов горизонтальным кием - подскока нет, так как отсутствует вертикальная составляющая в поступательном движении шара.
При ударе по битку наклонным кием, помимо горизонтальной составляющей в поступательном движении шара, возникает вертикальная составляющая, вызванная упругой реакцией плиты стола на кратковременное повышение давления на нее в момент удара.
Для ударов наклонным кием, где угол наклона кия и/или сила удара невелики подскок шара незначительный, и его влиянием можно пренебречь.
В иных случаях, т.е при ударах наклонным кием, где угол наклона кия и/или сила удара достаточно велики, это влияние необходимо учесть.
В этом случае движение шара разбивается на две фазы: период, когда шар находится в воздухе (фаза полета) и фаза удара о поверхность.
θi θi+1 Vi Vi+1 Fн^ Fтр^ θi+1 Vi+1
Координатные оси удобно взять так, что направление движения центра шара совпадает с положительным направлением оси Y, ось X - проведенная горизонтально перпендикулярно оси Y, ось Z - вертикально вверх. Координаты x и y лежат в поверхности, z перпендикулярно поверхности.]
Рассмотрим случай, когда шар не имеет вращения относительно оси OY (вращение массе) [т.е. удар в вертикальной плоскости, проходящей через центр шара].
Пусть, i=0 - 0-вое "падение", т.е удар наклонным кием.
Тогда, начальные параметры:
V0 - начальная поступательная скорость, приданная шару ударом кия (направлена под углом вниз).
ωx0 - начальная уговая скорость вращения относительно оси X
ωy0=0 - начальная уговая скорость вращения относительно оси Y отсутствует.
θ0 - угол наклона кия.

Фаза полета: Движение шара в этой фазе можно представить в виде суммы равномерного движения в горизонтальном направлении (если пренебречь сопротивлением воздуха, то на шар в горизонтальном направлении не действуют никакие силы) и равнопеременного движения в вертикальном направлении. Шар сначала взлетает, а потом падает и движение в вертикальной плоскости является сначала равнозамедленным (с ускорением -g), а потом равноускоренным (с ускорением g). В высшей точке полета вертикальная составляющая скорости обращается в ноль.
Величина скорости i-го отскока равна скорости (i+1)-го падения; угол i-го отскока равен углу (i+1)-го падения.
Движение шара в этой фазе описывается следующими уравнениями:
Горизонтальная составляющая скорости в момент времени t:
Vi+1*cos(θi+1)
Вертикальная составляющая скорости в момент времени t:
Vi+1*sin(θi+1)-g*t
Координата y в момент времени t:
y=Vi+1*cos(θi+1)*t
Координата z в момент времени t:
z=Vi+1*sin(θi+1)*t-g*t22
Высота подъема в высшей точке i-го полета:
hi=(Vi+1*sin(θi+1))22*g
Расстояние вдоль оси OY за время i-го полета (дальность i-го полета):
si=(Vi+1)2*sin(2*θi+1)g
Время полета i-го полета:
ti=2*Vi+1*sin(θi+1)g
Vi+1 - скорость шара сразу после i-го отскока и соответственно в момент i+1 падения.
θi+1 - угол i-го отскока и соответственно i+1 падения.
Вращение шара не изменяется за время полета.
ωxi+1 - угловая скорость шара относительно оси X в конце i-го отскока и соответственно i+1 падения.
[Высоту и длину полета регулируют силой удара и углом наклона кия.
С увеличением угла наклона кия высота полета увеличивается;
С увеличением силы удара (скорости шара) высота и длина полета увеличиваются
Например, чтобы ограничить длину полета, не уменьшая высоты полета можно увеличить угол наклона кия и уменьшить силу удара.
Скорость (Vi+1) и угол отскока (θi+1) , в свою очередь, зависят от силы удара, угла наклона кия и характера вращения шара.
На практике, высоты 1-2 диаметра шара соответствуют наклону кия в диапазоне от 30° до 50°.]
Фаза удара о поверхность:
Основные изменения поступательной и вращательной скорости происходят в фазе удара о поверхность. Удар — кратковременное взаимодействие тел, при котором происходит перераспределение кинетической энерги. Когда шар ударяется о поверхность, шар теряет кинетическую энергию. Кроме того, удар может придать шару некоторое вращение, преобразуя часть его поступательной кинетической энергии в кинетическую энергию вращения. Эти потери энергии обычно характеризуются (косвенно) через коэффициент восстановления (e).
В теории удара в качестве меры взаимодействия тел рассматривают не сами ударные силы, а их импульсы.
Ударная сила быстро возрастает от нуля в момент начала удара до максимального значения, затем так же быстро уменьшается обычно по другому закону до нуля в конце удара. Во многих случаях не требуется детального знания закона изменения ударной силы.
Применение законов сохранения энергии и импульса во многих случаях позволяет исключить из рассмотрения сам процесс столкновения и получить связь между скоростями тел до и после столкновения, минуя все промежуточные значения этих величин.
В данном случае достаточно рассмотреть ударные импульсы.
Изменение количества движения материальной точки за время удара равно ударному импульсу, приложенному к точке.
Проекции скорости материальной точки на оси координатной системы: Горизонтальная (тангенциальная) составляющая скорости в начале i-го удара:
Vti=Vyi=Vi*cos(θi)
Вертикальная (нормальная) составляющая скорости в начале i-го удара:
Vni=Vzi=(Vi*sin(θi))*(-1)
Составляющая скорости вдоль нормали при ударе меняет направление на противоположное.
Коэффициент восстановления (e) характеризует, насколько восстанавливается нормальная составляющая скорости после удара.
В конце удара нормальная составляющая скорости составит: Vni+1=Vzi+1=e*Vi*sin(θi)
Изменение импульса тела равно импульсу силы, действующей на него.
Разложим ударный импульс реакции поверхности на нормальную (вертикальную) и тангенциальную (горизонтальную, касательную) составляющие.
Нормальная составляющая (импульс силы нормальной реакции за время удара):
mш*Vzi+1-mш*Vzi =mш*e*Vi*sin(θi)-mш*(Vi*sin(θi))*(-1) =mш*(1+e)*Vi*sin(θi)
Тангенциальная и нормальная составляющие ударного импульса связаны коэффициентом ударного трения скольжения.
Тангенциальная составляющая (импульс силы трения за время удара): μск*(mш*(1+e)*Vi*sin(θi)) - при условии, что сила трения скольжения действует в течение всего времени удара
Однако сила трения скольжения действует только до тех пор, пока у шара есть ненулевая компонента относительной скорости вдоль поверхности.
    При начавшемся в начале удара скольжении шара сила трения одновременно начинает:
  1. изменять горизонтальную компоненту поступательной скорости
  2. изменять вращательную скорость шара
    3. Как только эти скорости сравняются по модулю и будут противоположны по направлению скольжение прекратится, далее шар просто катится.
  • Если шар движется вперед с обратным вращением, то скорости поступательного и вращательного движений будут сонаправлены.
    • Угловая скорость шара после удара уменьшится, как и его горизонтальная скорость, и шар поднимется вверх, возможно, даже превысив свою первоначальную высоту. Также возможно, что шар начнёт вращаться в противоположном направлении и даже отскочит назад.
  • Если шар движется вперед с прямым вращением, скорости поступательного и вращательного движений будут направлены в противоположные стороны.
    • Что именно произойдёт, зависит от того, какой из двух компонентов доминирует.
    -Если шар вращается быстрее, чем движется поступательно, то относительная скорость скольжения будет направлена в сторону скорости вращательного движения. А соответственно сила трения (ускорение) в сторону скорости поступательного движения. Угловая скорость шара после удара уменьшится, но его горизонтальная скорость увеличится. Шар будет двигаться вперёд, но не превысит своей первоначальной высоты и продолжит вращаться в том же направлении.
    - Если шар движется поступательно быстрее, чем вращается, то относительная скорость скольжения будет направлена в сторону скорости поступательного движения. А соответственно сила трения (ускорение) в сторону скорости вращательного движения. Угловая скорость шара после удара увеличится, но его горизонтальная скорость уменьшится. Шар не превысит свою первоначальную высоту и продолжит вращаться в том же направлении.
Касательно бильярда, ситуация когда шар отскочит назад не имеет смысла.
Таким образом,
  1. Если параметры удара такие,что за время i-го удара сила трения не успевает остановить скольжение, то:
    • Сила трения сообщает шару ускорение поступательного движения (F=m*a):
      За время i-го удара тангенциальная составляющая поступательной скорости (Vi*cos(θi)) изменится на величину: (μск*mш*(1+e)*Vi*sin(θi))mш=μск*(1+e)*Vi*sin(θi)
    • Сила трения создает момент силы, собщающий шару угловое ускорение (M=F*R=I*ε):
      За время i-го удара угловая вращательная скорость (ωxi) изменится на величину: (μск*mш*(1+e)*Vi*sin(θi))I/R=52*R(μск*(1+e)*Vi*sin(θi)) (aвр=ε*R)
      или линейная (тангенциальная) скорость вращательного движения (ωxi*R) изменится на величину:
      52(μск*(1+e)*Vi*sin(θi))
      • Уменьшатся/увеличатся поступательная/вращательная скорости зависит от направления силы трения.
      • В случае оттяжки (обратного вращения - поступательная и линейная вращательная скорости сонаправлены):
        {Vni+1=Vzi+1=-e*Vzi=e*Vi*sin(θi)Vti+1=Vyi+1=Vyi-(μск*(1+e)*Vi*sin(θi))=Vi*cos(θi)-(μск*(1+e)*Vi*sin(θi))ωxi+1*R=ωxi*R-52(μск*(1+e)*Vi*sin(θi))
      • В случае скользящего наката (поступательная и линейная вращательная скорости противоположно направлены; поступательная скорость больше вращательной):
        { Vni+1=Vzi+1=-e*Vzi=e*Vi*sin(θi) Vti+1=Vyi+1=Vyi-(μск*(1+e)*Vi*sin(θi))=Vi*cos(θi)-(μск*(1+e)*Vi*sin(θi)) ωxi+1*R=ωxi*R+52(μск*(1+e)*Vi*sin(θi))
      • В случае буксующего наката (поступательная и линейная вращательная скорости противоположно направлены; поступательная скорость меньше вращательной):
        { Vni+1=Vzi+1=-e*Vzi=e*Vi*sin(θi) Vti+1=Vyi+1=Vyi+(μск*(1+e)*Vi*sin(θi))=Vi*cos(θi)+(μск*(1+e)*Vi*sin(θi)) ωxi+1*R=ωxi*R-52(μск*(1+e)*Vi*sin(θi))
  2. Сила трения действует на шары, пока у шаров есть ненулевая компонента скорости.
    Условие прекращения скольжения за время удара: относительная скорость скольжения должна обратиться в нуль до конца удара. В этом случае относительное движение тел в точке контакта прекращается, а сила трения скольжения перестает действовать.
    Если параметры удара такие,что за время i-го удара сила трения успевает остановить скольжение, то сила трения скольжения перестает действовать.
    Как известно, финальная скорость шара (скорость к моменту финального качения) образуется на 57 от вектора начальной поступательной скорости (v_) и на 27 от вектора противоположного вектору начальной вращательной скорости ([ω_xR_])
    Таким образом, если (57Vi*cos(θi)-27ωxi*R)>Vi*cos(θi)-(μск*(1+e)*Vi*sin(θi)) (в случае обратного вращения / скользящего наката),
    (57Vi*cos(θi)-27ωxi*R)< Vi*cos(θi)+(μск*(1+e)*Vi*sin(θi)) (в случае буксующего наката),
    то
    {Vni+1=Vzi+1=-e*Vzi=e*Vi*sin(θi)Vyi+1=57Vi*cos(θi)-27ωxi*Rωxi+1=-Vyi+1
Скорость сразу после i-го удара (скорость отскока):
Vi+1=Vni+12+Vti+12
Угол отскока:
θi+1=arctg(Vni+1Vti+1)
Если начальные параметры удара таковы, что на шаре есть вращение относительно оси Y (вращение массе).
Тогда, начальные параметры:
V0 - начальная поступательная скорость, приданная шару ударом кия (направлена под углом вниз).
ωx0 - начальная уговая скорость вращения относительно оси X
ωy0 - начальная уговая скорость вращения относительно оси Y.
Тогда движение шара в горизонтальной плоскости (OXY) нужно рассмотреть как сумму движений по осям OX и OY. Начальные параметры будут:
  • по оси X: Vx0=0
    ωy0
  • по оси Y: Vy0=V0*cos(θ0)
    ωx0
  • θ0 - угол наклона кия.
Далее, алгоритм аналогичный, только в данном случае, т.е при ударе наклонным кием с боковой составляющей винта добавляется вращение шара вокруг оси Y (ωy), поэтому необходимо учесть два момента:
  1. В результате вращения тела вокруг оси Y возникает линейная скорость точки опоры (ωyR), направленная в каждый момент времени по касательной к окружности вращения, т.е вдоль оси X; сила трения от этого вращения разгоняет шар по оси X; движение в плоскости OXY складывается из движений по осям X и Y; тем самым тангенциальная (горизонтальная) составляющая поступательной скорости не коллинеарна оси Y.
    α1 - угол между вектором тангенциальной составляющей поступательной скорости и осью Y.
  2. вектора линейной вращательной скорости и тангенциальной составляющей поступательной скорости точки опоры шара не коллинеарны. Поэтому сила трения, направление которой противоположно результирующей скорости скольжения точки опоры шара (сумма векторов поступательного и вращательного движений) образует некоторый угол с направлением начального движения. Этот угол при движении шара остается постоянным, а относительная скорость скольжения за время скольжения упадет до нуля; после чего переменная фаза движения шара закончится - скольжение прекратится и шар перейдет в финальное состояние качения.
    α2 - угол между вектором относительной скорости скольжения и осью Y.
    3. [Вектор силы трения скольжения Fтр всегда направлен противоположно вектору скорости движения тела относительно соприкасающегося с ним тела (вектору относительной скорости скольжения).]
    [Углом между двумя векторами, отложенными от одной точки, называется кратчайший угол, на который нужно повернуть один из векторов вокруг своего начала до положения сонаправленности с другим вектором.
    Угол между векторами может быть положительным или отрицательным. Положительный угол соответствует "повороту" против часовой стрелки от первого вектора ко второму. Отрицательный угол, наоборот, соответствует "повороту" по часовой стрелке]
Фаза удара шара о поверхность.
На шаре обратное (нижнее) вращение (ωxR) плюс правое боковое вращение (ωyR).
[Т.е. удар наклонным кием ниже центра масс шара с правым боковиком]
➤
➤
➤
) α1
➤
➤
➤
➤
) α2
➤
➤
)
➤
Vx
Vy
Vxy=Vt
ωxR
ωyR
ωxyR
Vотн
Fтр
Vn
V
X
Y
Z
Vt_ = Vxy_ = Vx_ + Vy_
[ωxy_xR_] = [ωx_xR_] + [ωy_xR_]
Vотн_ = Vxy_ + [ωxy_xR_]
V_ = Vn_ + Vt_
∠θi+1
- угол наклона поступательной скорости V к плоскости OXY
1. Если сила трения не успеет остановить скольжение за время удара. Проекции тангенциальной составляющей поступательной скорости (Vti+1) [рассматриваются проекции импульса силы трения на оси OX, OY]:
ось OX:
{ Vtxi+1=Vxi+(μск*(1+e)*Vi*sin(θi))*sin(α2)=Vi*cos(θi)*sin(α1i)+(μск*(1+e)*Vi*sin(θi))*sin(α2) ωyi+1*R=ωyi*R-52(μск*(1+e)*Vi*sin(θi))*sin(α2)
ось OY:
{ Vtyi+1=Vyi-(μск*(1+e)*Vi*sin(θi))*cos(α2)=Vi*cos(θi)*cos(α1i)-(μск*(1+e)*Vi*sin(θi))*cos(α2) ωxi+1*R=ωxi*R-52(μск*(1+e)*Vi*sin(θi))*cos(α2) [Уменьшатся/увеличатся поступательная/вращательная скорости по оси OY зависит от направления силы трения.]
Vti+1=Vtxi+12+Vtyi+12
Нормальная составляющая поступательной скорости:
Vni+1=Vzi+1=-e*Vzi=e*Vi*sin(θi)
Vi+1=Vni+12+Vti+12
α1i+1=arctg(Vtxi+1Vtyi+1)
sin(α2)=Vотн0xVотн0
cos(α2)=Vотн0yVотн0
Vотн0- относительная скорость в точке контакта между битком и сукном (скорость скольжения)
Vотн0=Vотн0x2+Vотн0y2
Vотн0x - проекция скорости Vотн0- на ось OX;
Vотн0y - проекция скорости Vотн0- на ось OY;
Vотн0x=Vx0-R*ωy0; Vотн0y=Vy0+R*ωx0;
2. Если сила трения успевает остановить скольжение за время удара. по оси OX:
Vxi+1=57Vxi+27ωyi*R
ωyi+1=-Vxi+1
по оси OY:
Vyi+1=57Vyi-27ωxi*R
ωxi+1=-Vyi+1
Vti+1=Vxi+12+Vyi+12
Удар наклонным кием приведет к подскокам шара. Получив сверху ударный импульс от кия, а снизу практически такой же импульс от плиты, биток сжимается и подпрыгивает, как мячик. С увеличением угла наклона кия и/или силы удара фаза вертикальная составляющая в поступательном движении шара будет увеличиваться Таким образом, чем больше наклон кия и сила удара, тем подскок битка будет более выраженным, а фаза подскоков более длительная.
Существенный наклон кия (>20°) в бильярде применяют для выполнения двух видов ударов - массе и перескока (джамп-удар).
    Основное различие этих ударов заключается в следующем:
  • Наличие боковой составляющей винта При джамп-ударах наклонным кием ударяют таким образом, чтобы ось кия находилась в вертикальной плоскости удара, проходящей через центр. (Как правило, ось кия проходит через центр шара или несколько ниже (для существенных наклонов)).
    Наличие боковой составляющей нежелательно, так как шар отклоняется от прямолинейной траектории в сторону примененного бокового винта.
    Боковая составляющая винта при выполнении ударов массе - ключевой фактор.
    Удар массе можно рассматривать как комбинацию вращений вокруг 3-х осей: вращения вокруг горизонтальной оси (расположенной поперек направления поступательного движения шара) - прямое/обратное вращение, вращения вокруг вертикальной оси - боковое вращение, вращения вокруг горизонтальной оси (расположенной по направлению поступательного движения шара) - вращение массе. Этот последний тип вращения (массе) приводит к искривлению траектории движения шара. Направление силы трения скольжения, возникающей от вращения массе не совпадает с направлением поступательного движения и поэтому эта сила искривляет траекторию движения шара, пока шар не перестанет скользить и не покатится по прямой в новом направлении.
    То есть, когда исполняется джамп-удар цель - перепрыгнуть препятствие; когда исполняется массе цель - обойти препятствие по дуге.
  • Выраженность фазы подскоков шара
    • При исполнении массе подскоки шара нежелательны. Подскоки влияют на траекторию шара, несмотря на то,что направление финальной траектории практически не изменяется. (параллельно линии, идущей от точки опоры шара к той точке, в которой линия удара пересекает плоскость бильярдного сукна) Изменение формы кривой в фазе скольжения связано с тем, что шар за время подскоков в большей степени теряет поступательную (тангенциальную составляющую - Vп=V*cos(θ)) и вращательную скорости (ωx*R, ωy*R) чем если бы шар скользил все это время не отрываясь от земли. Эти существенные потери происходят во время ударов шара о поверхность.
    Details
    Рассмотрим тангенциальный импульс за время i-го удара: μск*mш*(1+e)*Vi*sin(θi) - при условии действия силы трения в течение всего времени i-го удара. (Дуговая траектория возникает только за время скольжения шара, как только шар достиг финальной стадии - шар катится по прямой)
    Время полета i-го полета: 2*Vi+1*sin(θi+1)g
    Ускорение поступательного движения в случае, когда шар скользит не отрываясь от поверхности: μск*g
    За время полета i-го полета, в случае если бы шар все это время скользил без отрыва от поверхности, импульс силы трения составит: mш*(2*Vi+1*sin(θi+1)g)*(μск*g)
    Таким образом, можно сравнить:
    μск*mш*(1+e)*Vi*sin(θi) ^ mш*(2*Vi+1*sin(θi+1)g)*(μск*g)
    sin(θi)=VniVi; sin(θi+1)=Vni+1Vi+1; Vni+1Vni=e, где e - коэффициент восстановления.
    (1+e)*Vni ^ 2*Vni+1
    (1+e) ^ 2*e
    (1-e)>0
    Тот факт, что шар за время подскоков в большей степени теряет вращательную и поступательную скорости в сравнении с движением шара без отрыва от стола объясняет, что траектория шара укорачивается и сдвигается в сторону примененного бокового винта. Это затрудняет контроль траектории движения битка. Поэтому выполнить массе с крутой дугой (т.е с большим наклоном кия) черезвычайно сложно. В основном эти удары для трюковых шоу, где удар многократно отрепетирован и заранее учтены все параметры удара.
    Воздействие кия на биток выражается исключительно в передаче импульса, которая происходит в период времени их контакта. При ударе кием по битку происходит двойной удар: один между кием и шаром, другой между шаром и поверхностью стола. Под действием вертикальной составляющей ударного импульса происходит взаимодействие между шаром и поверхностью стола.
    Поэтому для таких ударов - важно время контакта наклейки кия с битком. Для массе - чем дольше, тем лучше. За это время шар оказывается "зажатым" между кием и столом, тем самым частично "погашая" вертикальную составляющую ударного импульса. Для джамп-ударов - наоборот. То есть кий передаст шару большую часть ударного импульса до того, как начнется взаимодействие между шаром и поверхностью стола. Кий должен не мешать. Для реализации этих целей используют специальные кии, предназначеные для выполнения джамп-ударов и ударов массе. Также есть особенности в технике удара.
    Джамп-удар, как правило, выполняется специальным облегченным кием и резким движением с свободным расслабленным хватом с таким расчетом, чтобы под действием силы отдачи кий сразу же оскочил назад, не сталкиваясь повторно с подпрыгнувшим битком. Малый вес кия позволит легче разогнать кий, а также легче отражаться от битка, чтобы не создавать помех движению битка.
    Твёрдость материала битка много больше твёрдости материалов кия, в том числе и наклейки, а значит время контакта определяется в значительно большей степени временем деформации кия, чем битка. Следовательно, время контакта между кием и наклейкой можно варьировать изменяя только упругость материалов кия. По степени жесткости наклейки кия делятся на мягкие, средние и твердые. Твердые, как и следует из названия, более жесткие. Мягкие, наоборот, очень хорошо держат мел, дольше контактируют с шаром при ударе, благодаря чему позволяют выполнять более сложные удары с вращением При выполнении массе особенно важно обеспечить надежный контакт наклейки с битком и устойчивое направление движения кия. Cпециальные кии, предназначеные для массе ударов тяжелее чем стандартные; имеют мягкий тип наклейки; имеют большую площадь рабочей поверхности наклейки.
    Специальные кии, предназначеные для джамп ударов легче чем стандартные; имеют жесткий тип наклейки; имеют меньшую площадь рабочей поверхности наклейки.
Вид сверху (по направлению взгляда):
Вид прямо (фронтальный вид):
Наклон кия: 15
1
2
Вид сверху (по направлению взгляда):
Вид прямо (фронтальный вид):
Наклон кия: 20
1
2
Вид сверху (по направлению взгляда):
Вид прямо (фронтальный вид):
Наклон кия: 35
1
2
1 - идеальная кривая, где фаза подскока шара отсутствует, т.е шар не отрывается от поверхности стола.
2 - такой же удар с выраженной фазой подскока шара.
Для ударов массе важно ограничить подскоки шара и приблизить траекторию к траектории 1.
Единственное, что практически не изменяется - направление финальной траектории практически - параллельно линии, идущей от точки опоры шара к той точке, в которой линия удара пересекает плоскость бильярдного сукна.
Вид сбоку
b
y
s
Z
Y
θ
Вид сверху
a
y
s
Y
X
α
P
C
    Одинаковые финальные направления можно задавать с разной комбинацией
  • (.) удара с координатами (a,y,b)
  • и угла наклона кия (∠θ).
[можно увеличивать / уменьшать a двигаясь по отрезку PC; можно увеличивать / уменьшать b - изменяя угол наклона кия.
Очевидно, что чем больше a и меньше b, тем меньше требуемый наклон кия для данного финального направления]
Так как "лишний" наклон кия нежелателен, то задача сводится к тому, чтобы найти такие координаты (.) удара в пределах зоны кикса, которые обеспечивали бы требуемое финальное направление () и при этом наклон кия был бы минимальным из возможных.
dx 2 = ( sin(θ)* R2-a2-b2 - b*cos(θ) ) 2
dy 2 = dz 2 = a 2 ,
где dx, dy, dz - плечо силы относительно осей X,Y,Z.
dx 2 + dy 2 < ( 0.57 R ) 2 - зона кикса
tg(θ)= b+R |y|+s
a= s*tg(α)
|y|= R2-a2-b2
где (a,y,b) - координаты (.) удара;
∠α - угол между финальным направлением шара и осью Y (желаемое финальное направление шара)
∠θ - угол наклона кия, обеспечивающий желаемое финальное направление шара при заданной (.) удара
Таким образом, задача сводится к следующему: необходимо найти такие координаты (.) удара в пределах зоны кикса, которые обеспечат желаемое финальное направление шара при мининимально возможном угле наклона кия.
{ dx 2 + dy 2 < ( 0.57 R ) 2 tg(θ)= b+R |y|+s = tg(α)*(b+R) tg(α)*|y|+a
Таким образом, задавая разные углы α, т.е выбирая желаемое финальное направление можно найти такую точку удара, что необходимый угол наклона кия при этом будет минимальным.
№αθ
120°26°
240°43°
360°52°
480°55°
Вид сверху в перспективе взгляда.
(Если смотреть сверху, поднимая зону кикса на соответсвующий угол θ)
Масштаб дуги (длина дуги) криволинейной части задается силой удара.
Отсюда становится понятным еще одно правило бильярда. Удары массе лучше выполнять на предельных винтах (ближе к границе зоны кикса), выбирая траекторию битка изменением силы удара и наклона кия. В этом случае, подскок битка при ударе будет минимальным, и его влияние на траекторию битка можно не учитывать.
Когда есть необходимость, чтобы шар вначале удара имел выраженный подскок, дальнейшую часть криволинейной траектории скользил по дуге не отрываясь от стола, то такие удары известны как джамп-массе. Хотя на практике они используются крайне редко, так как контроль траектории битка в данном случае заметно усложняется.
Наклонной оттяжкой (т.е удар наклонным кием с нижним винтом без боковой составляющей винта) нельзя придать шару такое количество вращения, которое невозможно было бы задать горизонтальным ударом. Начальная скорость вращения определяется моментом силы. Момент силы относительно данной оси — это физическая величина, равная произведению модуля силы F на её плечо. При заданной силе удара количество вращения (в данном случае относительно оси OX), придаваемое шару ударом кия зависит исключительно от плеча силы относительно оси вращения (оси X). И в случае удара наклонным кием и в случае удара горизонтальным кием предельное расстояние линии удара от центра (т.е. плечо силы) будет одинаково (0.57R).
Но с увеличением наклона кия при одной и той же силе удара будет уменьшаться горизонтальная составляющая поступательной скорости шара. Горизонтальная составляющая в поступательном движении шара будет уменьшаться, в то время как вертикальная составляющая будет увеличиваться. То есть удар наклонным кием позволяет задать меньшую скорость движения вперед шара при том же количестве вращения. Также изменится траектория битка после соударения с ПШ. Наклонная оттяжка позволяет создавать быструю оттяжку (quick draw) при ударах на резке. Быстрая оттяжка (quick draw) - удар с оттяжкой на резке, при котором требуется заставить биток как можно раньше продвигаться назад от тангенсной линии. Цель достигается с увеличением интенсивности вращения по отношению к поступательной скорости.
Отношение интенсивности вращения к поступательной скорости (горизонтальная составляющая) битка: SRF= ωx*R Vп
Варианты оттяжки с одинаковым количеством нижнего вращения к моменту соударения, но разным SRF.
➤
- ωx*R - нижнее вращение на битке [до / сразу после] соударения
➤
- Vп*sin(φ) - поступательная скорость битка [сразу после] соударения (в направлении тангенсной линии)
φ - угол резки
Ось Y - направление движения битка до соударения
Быстрая оттяжка
SRF=2
Средняя оттяжка
SRF=1.5
Медленная оттяжка
SRF=0.75
Vотн Fтр φ финальное качение тангенсная линия
Производная в точке показывает скорость изменения функции в данной точке.
Чем быстрее растет или убывает функция (чем круче ее график), тем больше по модулю ее производная.
y`= Дельтаy Дельтаx
Соответственно, чем больше изменение по y и меньше изменение по x в единицу времени, тем более крутой будет дуговая траектория шара при оттяжке.
Соответственно, чем больше угол наклона силы трения к оси x и меньше к оси y, тем более крутой будет траектория оттяжки шара.
Наклон силы трения к оси x зависит от соотношения вращательной и поступательной скорости
То есть в случае наклонной оттяжки по сравнению с ударом горизонтальным кием с идентичными силой удара и плечом силы можно достичь большего отношения интенсивности вращения к тангенциальной составляющей поступательной скорости битка (SRF). При этом расстояние, которое пройдет шар до того, как сила трения полностью "съест" нижнее вращение будет меньшим по сравнению с ударом горизонтальным кием с теми же параметрами (сила удара и плечо силы).
Также будет меньшим и количество вращения на битке к моменту соударения с ПШ. Связано с тем, что шар за время подскоков (ударов о поверхность) в большей степени теряет поступательную и вращательную скорости, чем если бы шар скользил все это время не отрываясь от земли.
Details Надо отметить, что больший SRF-фактор при наклонной оттяжке по сравнению с ударом горизонтальным кием с теми же параметрами (сила удара и плечо силы) достигается при углах наклона кия более 20 и величине плеча, близкой к предельному значению (0.5R).
Зависимость SRF-фактора при наклонной оттяжке от угла наклона.
Для сравнения SRF-фактор при ударе горизонтальным кием.
SRF
θ
dR=0.5
dR=0.4
dR=0.3
- наклонный кий - горизонтальный кий
Пусть V0, ωx0*R - начальные поступательная, вращательная скорости шара, заданные ударом кия.
Если сила удара и плечо силы одинаковы и при ударе наклонным кием и при ударе горизонтальным кием, то эти скорости будут идентичны в обоих случаях. С той разницей, что в случае удара наклонным кием поступательная скорость будет направлена под углом (θ) к плоскости движения шара.
| ωx*R V | = ωx*R V = 52 dxR
sin(θi) = Vni Vi ; sin(θi+1) = Vni+1 Vi+1 ; Vni+1 Vni = e
--- [при наклонной оттяжке] Для сравнения возьмем скорость вращения и поступательную скорость (горизонтальная составляющая) шара сразу после первого удара о поверхность.
[При условии, что шар скользит в течение всего периода отскока. В обратном случае на шаре уже не обратное, а прямое вращение.]
SRF1= ωx1*R Vп1 = ωx0*R - 52 µ*(1+e) *V0* sin(θ0) V0*cos(θ0) - µ*(1+e) *V0* sin(θ0) = 52 ( d/R - µ*(1+e) *sin(θ0) cos(θ0) - µ*(1+e) *sin(θ0) )
--- [при ударе горизонтальным кием] При ударе горизонтальным кием шар имеет начальные скорость вращения [нижнее вращение] (>ωx0*R) и поступательную скорость V0. По мере движения шара эти скорости будут уменьшаться. В качестве ориентира времени возьмем время первого подскока (полета) шара в случае удара наклонным кием.
SRF2= ωx2*R Vп2 = ωx0*R - 52 (µ*g)* ( 2* V1* sin(θ1) /g ) V0 - (µ*g)* ( 2* V1* sin(θ1) /g ) = 52 ( V0*(d/R) - 2*µ*Vn1 V0 - 2*µ*Vn1 ) = 52 ( V0*(d/R) - 2*µ*V0*sin(θ0)*e V0 - 2*µ*V0*sin(θ0)*e ) = 52 ( d/R - 2*µ*sin(θ0)*e 1 - 2*µ*sin(θ0)*e )
Таким образом, единственное преимущество наклонной оттяжки в сравнении с горизонтальным ударом кия с теми же силой удара и плечом силы - это возможность увеличить отношение интенсивности вращения к поступательной скорости (горизонтальная составляющая) более определенного предельного значения, которое может дать удар горизонтальным кием с теми же условиями. Что позволит получить "быструю" оттяжку.
В остальном, для хорошей оттяжки удар горизонтальным кием предпочтителен. Поэтому, в бильярде соответствуют для хорошей оттяжки наносить удар горизонтальным кием ниже центра немного недоходя до границы зоны кикса.
В случае удара горизонтальным кием SRF-фактор будет увеличиваться при увеличении плеча силы (d), и наоборот.
Рассмотрим зависимость поступательной и вращательной скоростей шара от точки удара ((a,y,b) - координаты точки удара) при заданной скорости кия.
    Удар в системе (кий-шар) описывается тремя уравнениями:
  1. закон сохранения энергии
  2. закон сохранения импульса
  3. коэффициент восстановления энергии
1) закон сохранения энергии:
Ekин1= 12 mк* Vк2 - кинетическая энергия до удара
Ekин2= 12 mк* Vк12 + 12 mш* Vш2 + 12 I* ω2 - кинетическая энергия после удара
где:
mк, mш - массы кия и шара.
Vк, Vк1 - скорости кия до удара и после удара.
Vш - поступательная скорость шара после удара
I=25 mш*R2 - момент инерции шара относительно любой оси, проходящей через центр масс
ω - угловая скорость шара относительно мгновенной оси (сразу после удара), проходящей через центр масс.
Ekин1=Ekин2 [абсолютно упругое столкновение без потери энергии]
mк*Vк2 = mк*Vк12 + mш*Vш2 + 25*mш*(ω2*R2)
| ωR V | = 52 dR
где d - плечо силы F^ (ударный импульс) относительно центра масс шара (расстояние от мгновенной оси вращения [сразу после удара] до центра масс шара)
(ωRV) 2 = ( 52 dR ) 2
d (tip offset) = a2 + (sin(θ)*R2-a2-b2-b*cos(θ)) 2
|y|=R2-a2-b2
2) закон сохранения импульса:
F^= mк*Vк - mк*Vк1 = mш*Vш
Изменение импульса тела при действии на него силы равно импульсу этой силы
Vк1= Vк- mшmк Vш
3) коэффициент восстановления энергии:
Коэффициент восстановления энергии характеризует потери механической энергии соударяющихся тел вследствие появления в них остаточных деформаций и их нагревания.
Коэффициент восстановления энергии равен отношению суммарной кинетической энергии после удара к их кинетической суммарной энергии до удара.
η= Ekин2 Ekин1
η*mк*Vк2 = mк*Vк12 + mш*Vш2 + 25*mш * ( 52*Vш*dR ) 2
mшк= mш mк
η*Vк2 = Vк12 + mшк*Vш2 + mшк*52 *Vш2 * (dR) 2
Vк12= ( Vк- mшк*Vш ) 2
(1+mшк+52(dR)2) *Vш2 + (-2*Vк)*Vш + ( 1-η mшк Vк2 ) =0
Решая это квадратное уравнение по Vш:
Vш = Vк 1+ η- ( 1-η mшк ) * ( 1+52 (dR) 2 ) ( 1+mшк +52 (dR) 2 ) = f1(dR)
|ω*R| = 52VшdR = f1(dR) * f2(dR) ,
где d - плечо силы F^ относительно центра масс шара (расстояние от оси вращения до центра масс шара)
d (tip offset) = a2 + (sin(θ)*R2-a2-b2-b*cos(θ)) 2
Таким образом, зависимость вращательной скорости (ω*R) от скорости кия при заданном плече силы (dR) - линейная. То есть с увеличением скорости разгона кия вращательная и поступательная скорости линейно возрастают.
В то время как зависимость вращательной скорости от плеча силы (точки удара) при заданной скорости кия - не линейная. Данная функция сначала возрастает, принимает наибольшее значение, а потом убывает.
Тогда взяв производную по dR ( f1(dR) * f2(dR) ) ` и приравняв производную к нулю можно найти плечо силы F^ относительно центра масс при котором вращательная скорость ω*R будет максимальна при заданной скорости кия.
Этот показатель (dR) составляет 0.5, то есть очень близкий к границе кикса.
зависимость вращательной скорости от скорости кия при заданном плече силы
зависимость вращательной скорости от плеча силы (точки удара) при заданной скорости кия
Из графика зависимости вращательной скорости от плеча силы видно, что функция сначала растёт быстро, а затем, по мере приближения к своему максимуму, ее рост замедляется. Таким образом увеличение плеча силы (расстояния от линиии удара до центра) при приближении к границе зоны кикса дает незначительное увеличение вращательной скорости.
Отсюда следует, что для того, чтобы увеличить вращательную скорость при ударе надежнее наносить удар на небольшом расстоянии от границы зоны кикса, и просто добавить немного силы удара для достижения оптимального эффекта.
Также нет смысла наносить удар на предельном расстоянии (близком к границе зоны кикса) при желании "донести" максимальное количество нижнего вращения до далекого прицельного шара. При одной и той же скорости кия: чем дальше точка удара от центра шара, тем меньше будет приданного поступательного движения при увеличении вращательного движения. При этом скорость вращения при приближении к границе зоны кикса увеличивается незначительно. Уменьшение поступательной скорости приведет к тому, что шару понадобится больше времени для того, чтобы достичь прицельный шар; а за это время сила трения, действующая в каждый момент времени "съест" большую часть нижнего вращения.
В бильярде рекомендуют для того чтобы донести максимальное нижнее вращение до отдаленного ПШ наносить удар на расстоянии 70-80% (0.35R-0.4R) от предельной величины плеча силы.
Плотность контакта
3/4
2/4
1/4
7/8
6/8
5/8
4/8
3/8
2/8
1/8
A
B
C
D
E
φ
fr - доля видимого горизонтального диаметра ПШ (1/4,2/4 и т.д)
∠ φ - угол резки
AB=AE+EB;
AE=R; EB=DB-DE;
DB=R; DE=fr*(2*R);
EB=R-fr*(2*R);
AB=R+R-fr*(2*R)=2*R*(1-fr);
AC=2*R;
∠ φ = asin ( ABAC ) = asin ( 2*R*(1-fr)2*R ) = asin ( 1-fr )

Правила (секреты) бильярда

В основном, все правила (рекомендации) бильярда расчитаны, что биток к моменту соударения находится в состоянии естественного качения. При естественном накате продольная скорость вращения ( |ωxy*R| = (ωx*R) 2 + (ωy*R) 2 ) равна по модулю и противоположна по направлению поступательной скорости шара ( Vxy = Vx2 + Vy2 ).
Также для анализа траектории битка, удобно направить ось Y - по направлению движению битка до соударения, ось X - перпендикулярно ей в горизонтальной плоскости. Тогда, Vx=0, ωy*R=0
ωx*R=-Vy
При естественном накате отношение скорости поступательного движения к скорости вращения остается все время постоянным, не зависимо от величины скорости. То есть трение качения уменьшает и скорость поступательного движения и скорость вращения, но по модулю они остаются равными в любой момент времени в фазе качения шара.
Правило 30 градусов

Правило, устанавливающее, что после соударения естественно катящегося битка с ПШ, происходящего при плотности контакта от четверти (1/4) до трех четвертей (3/4) шара, траектория битка отклоняется примерно на 30° от направления его поступательного перемещения непосредственно перед соударением (финальное отклонение битка).

Правило 90 градусов

Правило, устанавливающее, что после соударения, в момент которого биток не имеет продольного вращения (ωx=0) - плоский удар - шары расходятся под углом 90°.

Правило 3x

Правило, устанавливающее, что при толстом соударении (более чем в три четверти (3/4) шара) угол отражения битка примерно в 2.5-3 раза превышает угол резки.

Правило 70%

Правило, устанавливающее, что после тонкого соударения (менее чем в четверть (1/4) шара), произошедшего в состоянии естественного качения, биток отражается под углом составляющим примерно 70% угла между направлением движения непосредственно перед соударением и тангенциальной линией.

Правило trisect

Для ударов с "хорошей" оттяжкой на резке от 0 до 40 угол финального отклонения битка будет примерно в 3 раза больше угла резки.
"Хорошая" оттяжка - это значит не слишком мало и не слишком много нижнего вращения на шаре.
Вращение определяется моментом силы, скалярное значение которого равно произведению силы на плечо силы. Таким образом, все зависит от такого насколько сильно и как низко нанесен удар. Также необходимо учитывать и расстояние до ПШ, т.е. понимать какое количество нижнего вращения останется на битке к моменту соударения с ПШ.

Правило trisect |RωxV|=0.55
Правило trisect |RωxV|=0.6
Правило trisect |RωxV|=0.7
Правило ...

Правило, устанавливающее, что после соударения , произошедшего в состоянии естественного качения (тихий естественный накат), финальное направление движения битка проходит через 2/7 отрезка между тангенсной линией и линией прицеливания (направление движения битка до соударения), построенного перпендикулярно тангенсной линии.

[Важно отметить, что для этого правила тангенсная линия и линия прицеливания откладываются от той точки, где биток после соударения с ПШ перейдет в финальное состояние качения, т.е. будет двигаться по прямой в финальном направлении.
Поэтому, это правило удобно использовать для тихого естественного наката битка к моменту соударения с ПШ, когда после соударения с ПШ криволинейная часть траектории битка минимальна и биток практически сразу переходит в состояние естественного качения в финальном направлении.]
} }
27
57
O
A
B
C
) δ
) φ
CBAB = tg(∠COB) tg(∠AOB)
∠ φ - угол резки, ∠ δ - угол финального отклонения битка
OB - тангенсная линия, OA - линия прицеливания, OC - финальное направление битка
∠AOB=90-φ, ∠COB=90-φ-δ=90-(φ+δ)
Финальная скорость (скорость к моменту окончания скольжения) образуется на 5/7 от вектора начальной поступательной скорости в направлении тангенсной линии и на 2/7 от вектора противоположного вектору начальной скорости вращения.
По осям вращения (с учетом направления осей):
{ Vxf = 57 Vx0 + 27 ωy0 *R Vyf = 57 Vy0 - 27 ωx0 *R ,
где Vx0, Vy0 - проекции скорости V0.
V0 - поступательная скорость битка сразу после соударения (в направлении тангенсной линии).
V0=V*sin(φ)
V - поступательная скорость битка к моменту соударения (в направлении линии прицеливания)
{ Vx0 = V*sin(φ)*cos(φ) Vy0 = V*sin(φ)*sin(φ)
ωx0, ωy0 - угловые скорости вращения к моменту (сразу после) соударения.
Ось Y направлена по линии прицеливания, ось X - перпендикулярно ей.
Финальный угол отклонения битка можно найти, посмотрев наклон траектории в момент времени окончания скольжения.
δ= arctg ( Vxf Vyf ) = arctg ( 57 Vx0 + 27 ωy0 *R 57 Vy0 - 27 ωx0 *R )
Учитывая, что биток находится в состоянии естественного качения (ωx0 *R=-V) и биток не имеет вращения относительно оси Y (ωy0=0, что означает удар только с накатом, оттяжкой или клапштос).
Тогда, δ= arctg ( 5*sin(φ)*cos(φ) 5* sin 2 (φ) +2 )
Тогда,
CBAB = tg(∠COB) tg(∠AOB) = tg(90-φ-δ) tg(90-φ) = tg(φ)* ( 1- tg(φ)*tg(δ) ) tg(φ)+tg(δ)
Подставив в это выражение tg(δ) и упростив получим:
CBAB = 27
Угол финального отклонения - угол, который скорость своего шара в финальном состоянии (качения) после удара о прицельный шар образует с направлением его движения до удара.
Для наката угол финального отклонения называется углом прокатки, для оттяжки - углом отката.
фаза скольжения
фаза качения
угол финального отклонения
δ
Для естественно катящегося битка к моменту соударения с ПШ угол финального отклонения есть функция от аргумента φ (угол резки).
δ= f(u(φ)) = arctg ( 5*sin(φ)*cos(φ) 5* sin 2 (φ) +2 )
Это выражение может дать ряд интересных закономерностей.
1) При заданном угле резки качение битка после некоторой фазы скольжения будет происходить по прямой линии, расположенной под одинаковым углом к направлению его движения до удара не зависимо от силы удара. То есть угол прокатки при заданном угле резки (плотность удара) будет одинаков для любой скорости естественно катящегося битка непосредственно перед соударением. То есть если биток успевает перейти в фазу качения к моменту соударения с ПШ, то сила удара не влияет на угол прокатки.
Разница будет только в длине фазы скольжения [форма кривой траектории скольжения битка будет одинакова, только разного масштаба].
2) Угол прокатки зависит от величины резки, увеличиваясь от нуля при резке "в лоб" (∠ φ=0) (прокатка вслед ПШ), а затем уменьшаясь обратно до нуля при резке "воздухом" (прокатка без отклонения). Максимальный угол прокатки 34° (∠ δ=34°) соответствует резке чуть толще чем в полшара.
Для того,чтобы найти угол резки (∠ φ) для максимального угла прокатки возьмем производную fφ ` = (f(u(φ))) ` = fu ` * uφ ` .
Для того, чтобы функция имела экстремум необходимо, чтобы производная этой функции была равна нулю. Для этого достаточно рассмотреть uφ`=0
(u(φ)) ` = ( 5*sin(φ)*cos(φ) 5* sin 2 (φ) +2 ) ` = ( cos2(φ) - sin2(φ) ) * (sin2(φ)+2/5) - 2*sin2(φ)*cos2(φ) (sin2(φ)+2/5) 2 = 0
Приравняв к нулю числитель получаем ∠ φ ≈ 28°
δ= f(u(φ)) = arctg ( 5*sin(28)*cos(28) 5* sin 2 (28) +2 ) ≈ 34°
Построим график функции f(u(φ))
угол резки
угол прокатки
Таким образом видно, что наибольшую крутизну функция имеет на отрезке, ∠ φ от 0 до 17°. То есть погрешность в резке, приведет к более существенному отклонению от желаемого угла прокатки битка.
Поэтому, считается, что сыграть биток накатом при толстой резке значительно труднее, чем при резке в полшара.